Secara umum, orang mengetahui bila hendak menghubungkan dua buah komputer atau menghubungkan dua buah HUB/switch dengan kabel UTP, orang akan menggunakan kabel crossover. Dan bila hendak menghubungkan komputer ke HUB/switch,

orang akan menggunakan kabel straight.

Nah, sebelum bicara masalah pengkabelan straight dan crossover, kita lihat standar yang sudah ditetapkan untuk masalah pengkabelan ini, EIA/TIA 568A dan EIA/TIA 568B.

EIA/TIA 568A

EIA/TIA 568B

Kabel Straight

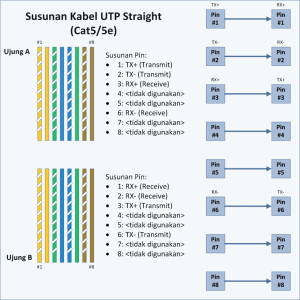
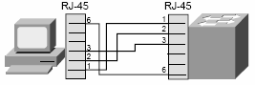
Kabel straight adalah istilah untuk kabel yang menggunakan standar yang sama pada kedua ujung kabel nya, bisa EIA/TIA 568A atau EIA/TIA 568B pada kedua ujung kabel. Sederhananya, urutan warna pada kedua ujung kabel sama. Pada kabel straight, pin 1 di salah satu ujung kabel terhubung ke pin 1 pada ujung lainnya, pin 2 terhubung ke pin 2 di ujung lainnya, dan seterusnya.
Jadi, ketika PC mengirim data pada pin 1 dan 2 lewat kabel straight ke switch, switch menerima data pada pin 1 dan 2. Nah, karena pin 1 dan 2 pada switch tidak akan digunakan untuk mengirim data sebagaimana halnya pin 1 dan 2 pada PC, maka switch

menggunakan pin 3 dan 6 untuk mengirim data ke PC, karena PC menerima data pada pin 3 dan

                                                                              6.

Lebih detailnya, lihat gambar berikut :

Penggunaan kabel straight :

• menghubungkan komputer ke port biasa di switch.
• menghubungkan komputer ke port LAN modem cable/DSL.
• menghubungkan port WAN router ke port LAN modem cable/DSL.
• menghubungkan port LAN router ke port uplink di switch.
• menghubungkan 2 HUB/switch dengan salah satu HUB/switch menggunakan port uplink dan yang lainnya menggunakan port biasa

Kabel crossover
Kabel crossover menggunakan EIA/TIA 568A pada salah satu ujung kabelnya dan EIA/TIA 568B pada ujung kabel lainnya.
Pada gambar, pin 1 dan 2 di ujung A terhubung ke pin 3 dan 6 di ujung B, begitu pula pin 1 dan 2 di ujung B yang terhubung ke pin 3 dan 6 di ujung A. Jadi, pin 1 dan 2 pada setiap ujung kabel digunakan untuk mengirim data, sedangkan pin 3 dan 6 pada setiap ujung kabel digunakan untuk menerima data, karena pin 1 dan 2 saling terhubung secara bersebrangan dengan pin 3 dan 6.
Nah, coba bayangkan kalau untuk menghubungkan sebuah komputer ke HUB/switch menggunakan kabel crossover. Pin 1 dan 2 pada komputer digunakan untuk mengirim data, sedangkan 3 dan 6 pada HUB/switch juga digunakan untuk mengirim data, tapi karena kabel yang digunakan adalah crossover dimana pin 1 dan 2 (komputer) pada salah satu ujungnya terhubung ke pin 3 dan 6 pada ujung lainnya (HUB/switch) maka keduanya mengirim data pada jalur yang sama (*silahkan pikirkan sendiri).
Jadi teringat masa lalu, cara saya untuk mengenali sebuah kabel apakah crossover ataupun straight adalah dengan hanya melihat salah satu ujung kabel. Jika urutan warna kabel pada pin 1 adalah Putih Hijau, maka kabel tersebut adalah kabel crossover (*padahal jika ujung yang satunya lagi juga memiliki urutan warna yang sama yaitu Putih Hijau sebagai pin 1, maka kabel tersebut adalah kabel Straight). Tapi untungnya, kebanyakan kabel menggunakan standar EIA/TIA 568B pada kedua ujung kabelnya, jadi ketika saya ditanya apakah kabel itu straight ataupun crossover, saya tidak pernah salah menjawab (*walaupun salah mengerti). Maklum, ilmu yang disediakan di sekolah memang cukup sedikit tapi tidak demikian dengan Google.
Penggunaan kabel crossover :

• menghubungkan 2 buah komputer secara langsung
• menghubungkan 2 buah HUB/switch menggunakan port biasa diantara kedua HUB/switch.
• menghubungkan komputer ke port uplink switch
• menghubungkan port LAN router ke port biasa di HUB/switch

Port biasa vs. port uplink

Pada umumnya, untuk menghubungkan dua buah HUB/switch atau menghubungkan dua buah komputer secara langsung dibutuhkan kabel crossover. Tapi jika HUB/switch atau Network Interface Card (NIC) atau peralatan network lainnya menyediakan Uplink
port atau MDI/MDI-X anda bisa menggunakan kabel straight untuk menghubungkan ke port biasa di HUB/switch atau Network Interface Card atau peralatan network lainnya (*peralatan yang sejenis).

1.Masukkan CD Installer ke perangkat CD / DVD-ROM dan reboot komputer untuk boot dari CD.
Tunggu sampai CD termuat ...

2.Anda akan melihat wallpaper dan jendela instalasi. Pilih bahasa dan klik tombol "Install Ubuntu 10.04
LTS" untuk melanjutkan ..

3.Layar kedua akan menampilkan peta bumi. Setelah pemilihan lokasi, waktu sistem akan menyesuaikan.
Klik tombol "Forward" setelah Anda memilih lokasi yang Anda inginkan ..

4.Pada layar ketiga, Anda dapat memilih layout keyboard yang diinginkan.
Klik tombol "Forward" bila Anda telah selesai dengan konfigurasi keyboard ...

5.Anda memiliki empat pilihan di sini:

  Jika Anda memiliki sistem operasi lain (misalnya Windows XP) dan Anda ingin sistem dual boot, pilih :

1. Pilihan pertama : "Instal mereka berdampingan, memilih di antara mereka pada setiap startup."
2. Pilihan Kedua : "Jika Anda ingin menghapus sistem operasi yang ada, atau hard drive sudah kosong dan Anda ingin agar installer secara otomatis mempartisi hard drive Anda, pilih pilihan kedua, "Gunakan seluruh disk (Use entire disk)"
3. Pilihan Ketiga : "Gunakan ruang terbesar bebas terus-menerus" dan akan menginstal Ubuntu 10.04 di ruang unpartitioned pada hard drive yang dipilih.
4. Pilihan Keempat : "Tentukan partisi secara manual" dan dianjurkan HANYA untuk pengguna tingkat lanjut, untuk membuat partisi khusus atau memformat hard drive dengan filesystem lain dari yang default. Tetapi juga dapat digunakan untuk menciptakan partisi / home, yang sangat berguna jika Anda menginstal ulang seluruh sistem.

6.Tabel partisi akan terlihat seperti gbr di atas. Klik tombol "Forward" untuk melanjutkan instalasi ...

7.Pada layar ini, isi kolom dengan nama asli Anda, nama yang ingin Anda gunakan untuk login di Ubuntu
OS (juga dikenal sebagai username yang akan diminta untuk log in ke sistem), password dan nama
komputer (secara otomatis, tetapi bisa ditimpa).

8.Juga pada langkah ini, ada sebuah opsi bernama "Login secara otomatis". Jika Anda mencentang kotak
pada pilihan ini, Anda akan secara otomatis login ke desktop Ubuntu. Klik tombol "Forward" tombol
untuk melanjutkan ...

9.Ini adalah langkah akhir instalasi. Klik tombol “Install”.

10.Ubuntu 10.04 LTS (Lucid Lynx) akan terinstall...

11.Setelah beberapa menit (tergantung spesifikasi komputer Anda), sebuah jendela pop-up akan muncul,
yang memberitahukan bahwa instalasi selesai, dan Anda harus me-restart komputer untuk
menggunakan sistem operasi Ubuntu yang baru diinstal. Klik tombol "Restart Now"...

12.CD tersebut akan keluar otomatis; keluarkan dan tekan "Enter" untuk reboot. Komputer akan direstart
dan dalam beberapa detik, Anda akan melihat boot splash Ubuntu ...

13.Pada layar login, klik nama pengguna Anda dan masukan password Anda.
Klik "Log In" atau tekan Enter ...

14.Tampilan Desktop Ubuntu 10.04 LTS (Lucid Lynx).

OPERASI PENJUMLAHAN BILANGAN BINER

Operasi aritmatika seperti penjumlahan pada bilangan desimal adalah biasa bagi kita, tetapi bagaimana dengan operasi penjumlahan pada bilangan biner? Pada bilangan biner yang hanya terdiri dari dua sistem bilangan (‘0’ dan ‘1’), tentu-nya operasi penjumlahan terhadap bilangan biner akan lebih sederhana, contoh:

0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10
1 + 1 + 1 = 11

Sama hal-nya seperti pada operasi aritmatika penjumlahan pada bilangan desimal dimana bila ada hasil penjumlahan yang hasilnya dua digit, maka angka paling sebelah kiri akan dijumlahkan pada bilangan berikutnya atau dikenal dengan istilah ‘Disimpan’. Sebagai contoh perhatikan penjumlahan bilangan biner berikut ini.

              11  1   ←  (disimpan)  →   1
010101       1001001                 001101
100010       0011001                 100001
------(+)    -------(+)              ------(+)
110111       1100010                 101110

OPERASI PENGURANGAN BILANGAN BINER

Operasi aritmatika pengurangan pada bilangan biner juga sama seperti operasi pengurangan pada bilangan desimal, sebagai contoh perhatikan operasi dasar pengurangan bilangan biner berikut ini.

0 – 0 = 0
1 – 0 = 1
0 – 1 = 1 → bit ‘0’ meminjam 1 dari bit di sebelah kiri-nya
1 – 1 = 0

Contoh: Pengurangan 37 - 17 = 20 (desimal) atau 100101 - 010001 = 010100 (biner)

 1 → pinjam
100101 = 37
010001 = 17
-----------(-)
010100 = 20

Untuk menyatakan suatu bilangan desimal yang bernilai negatif adalah dengan menambahkan tanda negatif (-) pada bilangan-nya, contoh -1, -2, -3, -4, -5 dan seterusnya. Tetapi pada bilangan biner ini tidak bisa dilakukan, lalu bagaimana untuk membuat atau membedakan suatu bilangan biner itu bernilai negatif (-).
Ada beberapa cara untuk membuat suatu bilangan biner bernilai negatif, cara yang pertama adalah dengan menambahkan ekstra bit pada bagian paling sebelah kiri bilangan (Most Significant Bit / MSB), contoh;
101 = +5 
Dengan menambahkan ekstra bit: 
0101 = +5 → 0 merupakan ekstra bit (MSB) untuk tanda positif (+) 
1101 = -5 → 1 merupakan ekstra bit (MSB) untuk tanda negatif (-)
Cara seperti di atas ternyata dapat menimbulkan salah persepsi jika kita tidak cermat, karena nilai -5 = 1101, 1101 dapat diartikan juga sebagai bilangan 13 dalam bilangan desimal. Maka digunakan cara kedua yaitu menggunakan satu metode yang dinamakan ‘Komplemen Dua’. Komplemen dua merupakan komplemen satu (yaitu dengan merubah bit ‘0’ menjadi ‘1’ dan bit ‘1’ menjadi ‘0’) kemudian ditambah satu, contoh;

0101 = +5 → ubah ke bentuk komplemen satu
1010 → komplemen satu dari 101 ini kemudian ditambahkan 1
   1
----(+)
1111 → ini merupakan bentuk komplemen dua dari 0101 yang bernilai -5

Contoh lain, berapakah nilai -7 pada bilangan biner?

0111 = +7
1000 → bentuk komplemen satu
   1
----(+)
1001 → bentuk komplemen dua dari 0111 yang bernilai -7

Berikut tabel dari perbandingan bilangan biner original dengan bilangan biner dalam bentuk komplemen dua.

Sedangkan contoh untuk operasi pengurangan menggunakan metode komplemen dua sebenarnya adalah operasi penjumlahan bilangan biner, perhatikan contoh berikut.
Contoh; hasil penjumlahan +6 + (– 4) = 2 (desimal), bagaimana jika dalam operasi penjumlahan bilangan biner (komplemen dua)?

Jawab: Pertama kita cari bentuk komplemen dua dari +4

0100 = +4
1011 → komplemen satu dari 1100
   1
----(+)
100 → komplemen dua dari 100

Lalu jumlahkan +6 = 110 dengan -4 = (100)

110
100
---(+)
010 = +2 → hasil penjumlahan 110 (+6) dengan 100 (-4)

Yang perlu diperhatikan dari operasi pengurangan bilangan biner menggunakan metode komplemen dua adalah jumlah bit-nya. Pada contoh di atas semua operasi pengurangan menggunakan bilangan biner 3 bit (bit = binary digit), maksudnya disini adalah jika bilangan biner yang dihitung merupakan bilangan biner 3 bit maka hasilnya harus 3 bit. Seperti pada pengurangan 110 dengan 100 dimana pada digit paling sebelah kiri (MSB) pada kedua bilangan biner yakni ‘1’ dan ‘1’ jika dijumlahkan hasilnya adalah ‘10’ tetapi hanya digit ‘0’ yang digunakan dan digit ‘1’ diabaikan.

1
 110
 100
----(+)
1010 → ‘1’ pada MSB diabaikan pada operasi pengurangan biner komplemen dua

Contoh lain hasil pengurangan bilangan desimal 3 – 5 = -2 jika dalam biner.

11
011 → bilangan biner +3
011 → komplemen dua bernilai -5
---(+)
110 → hasilnya = -2 (komplemen dua dari +2)

Untuk mengetahui apakah 110 benar-benar merupakan nilai komplemen dua dari +2 cara-nya sama seperti kita merubah dari biner positif ke biner negatif menggunakan metode komplemen dua. Perhatikan operasi-nya berikut ini.

110 = -2
001 → komplemen satu dari 110
  1
---(+)
010 → komplemen dua dari 110 yang bernilai +2

Dari contoh semua operasi perhitungan di atas dapat ditarik kesimpulan bahwa komplemen dua dapat digunakan untuk mengetahui nilai negatif dan nilai positif pada operasi pengurangan bilangan biner.

OPERASI PERKALIAN BILANGAN BINER

Sama seperti operasi perkalian pada bilangan desimal, operasi aritmatika perkalian bilangan biner pun menggunakan metode yang sama. Contoh operasi dasar perkalian bilangan biner.

0 x 0 = 0
0 x 1 = 0
1 x 0 = 0
1 x 1 = 1

Contoh perkalian 12 x 10 = 120 dalam desimal dan biner.

Dalam operasi bilangan desimal;

 12
 10
 ---(x)
 00
12
----(+)
120

Dalam operasi bilangan biner;

   1100 = 12
   1010 = 10
   ----(x)
   0000
  1100
 0000
1100
-------(+)
1111000 = 120

OPERASI PEMBAGIAN BILANGAN BINER

Operasi aritmatika pembagian bilangan biner menggunakan prinsip yang sama dengan operasi pembagian bilangan desimal dimana di dalamnya melibatkan operasi perkalian dan pengurangan bilangan.
Contoh pembagian 9 : 3 = 3 (desimal) atau 1001 : 11 = 11 (biner)

     ____
11 / 1001 \ 11 → Jawaban
      11
      ---(-)
       11
       11
       ---(-)
        0

Contoh pembagian 42 : 7 = 6 (desimal) atau 101010 : 110 = 111 (biner)

     _______
110 / 101010 \ 111 → Jawaban
       110
       ------(-)
        1001
         110
        ------(-)
          110
          110
          ----(-)
            0

BCD (BINARY CODED DECIMAL)          

BCD adalah sistem pengkodean bilangan desimal yang metodenya mirip dengan bilangan biner biasa; hanya saja dalam proses konversi, setiap simbol dari bilangan desimal dikonversi satu per satu, bukan secara keseluruhan seperti konversi bilangan desimal ke biner biasa. Hal ini lebih bertujuan untuk “menyeimbangkan” antara kurang fasihnya manusia pada umumnya untuk melakukan proses konversi dari desimal ke biner -dan- keterbatasan komputer yang hanya bisa mengolah bilangan biner. Untuk lebih jelas, dapat dilihat pada contoh berikut :

Misalkan bilangan yang ingin dikonversi adalah 170₁₀.
Sesuai dengan posting saya yang sebelumnya, dapat dilihat bahwa bilangan biner dari :
1₁₀—-> 0001₂
7₁₀—-> 0111₂
0₁₀—-> 0000₂

Tetapi, berhubung hasil yang diinginkan adalah bilangan BCD, maka basis bilangannya tinggal ditulis sebagai berikut :
1₁₀—-> 0001_BCD
7₁₀—-> 0111_BCD
0₁₀—-> 0000_BCD

maka, nilai BCD dari 170₁₀ adalah 0001 0111 0000_BCD.
Harap diperhatikan bahwa setiap simbol dari bilangan desimal dikonversi menjadi 4 bit bilangan BCD.

Contoh lain, misalkan bilangan yang ingin dikonversi adalah 309₁₀.
3₁₀—–> 0011_BCD
0₁₀—–> 0000_BCD
9₁₀ —–> 1001_BCD
maka, nilai BCD dari 309₁₀ adalah 0011 0000 1001_BCD.

Sebagai bahan latihan, dapat juga dicoba konversi BCD bilangan desimal berikut :
10₁₀—–> 0001 0000_BCD
441₁₀—-> 0100 0100 0001_BCD
270₁₀—-> 0010 0111 0000_BCD

                                                         SISTEM BILANGAN DIGITAL

        Sistem Digital adalah suatu sistem yang berfungsi untuk mengukur suatu nilai atau besaran yang bersifat tetap atau tidak teratur dalam bentuk diskrit berupa digit digit atau angka angka .Biasanya sebelum mempelajari lebih dalam tentang sistem digital  pertama pasti kita akan mempelajari yang namanya Sistem Bilangan ,ada 4 jenis sistem bilangan yaitu biner ,oktal ,desimal ,hexadesimal .

1. Bilangan Biner adalah bilangan yang hanya punya basis 2 atau bilangan basis 2 ,yaitu 0 dan 1
2. Bilangan Oktal adalah bilangan yang hanya punya basis 8 atau bilangan basis 8 , yaitu 0,……,7
3. Bilangan Desimal adalah bilangan yang hanya punya basis 10 atau bilangan basis 10 ,yaitu 0,…….9
4. Bilangan Hexadesimal adalah bilangan yang hanya punya basis 16 atau bilangan basis 16 ,yaitu 0,……..9 ,A ,B ,C ,D ,E ,F (A=10 ,B=11 ,C=12 ,D=13 ,E=14 ,F=15)

Konversi Bilangan  adalah mengubah suatu sistem bilangan menjadi sistem bilangan lain.

Biner

*Biner ke Oktal

Caranya mudah ,kita hanya menyekatnya atau mengelompokkan berisi 3 bit bilangan ,dalam bentuk bilangan oktal ,111 = 4+2+1 = 7 ,sistem oktal ini disebut sistem 421.

Contoh :

110011010(2) = 110 011 010 = 4+2+0  0+2+1  0+2+0  = 632(8)

*Biner ke Desimal

Kita hanya tinggal mengalikan setiap bitnya dengan 2n  ,n = posisi bit ,MSB berarti pangkatnya paling besar sedangkan LSB pangkatnya paling kecil atau = 0, lalu hasilnya dijumlahkan .

Contoh :

110011010(2) = (1×28) + (1×27) + (0×26) +(0×25) + (1×24) + (1×23) + (0×22) + (1×21) +(0×20)

=   256  +   128   +    0     +    0     +    16    +    8      +    0     +    2     +   0 = 410(10)

*Biner ke Hexadesimal

Caranya mudah ,kita hanya menyekatnya atau mengelompokkan berisi 3 bit bilangan ,dalam bentuk bilangan oktal ,1111 = 8+4+2+1 = 15/F ,sistem hexadesimal ini disebut sistem 8421.

Contoh :

110110011010(2) = 1101  1001 1010 = 8+4+0+1  8+0+0+1  8+0+2+0 = 13  9  10 = D9A(16)

Oktal

*Oktal ke Desimal

Kita hanya tinggal mengalikan angka paling kiri dengan 8n , n adalah jumlah pangkaat tertinggi . MSB berarti pangkatnya paling besar sedangkan LSB pangkatnya paling kecil atau = 0, lalu hasilnya dijumlahkan .

Contoh :

678(8) = 6×82  7×81  8×80 = 6×64 + 7×8 + 8×1 = 384 + 56 + 8 = 440(10)

*Oktal ke Biner

Pada konversi bilangan oktal ke biner ini maksimal hanya angka misalnya 777(8) yang dapat langsung dikonversikan kebiner dengan cara sekat 7 = 111 , 7 = 111 , 7 = 111 jadi 777(8) =111111111(2) ,jika 777 keatas sudah tidak bisa menggunakan cara ini ,harus diubah kedesimal dahulu baru bisa langsung ke biner.

Contoh :

653(8) = ( dengan cara sekat langsung karena tidak ada angka yang >7 )

653(8) = 6 = 110 ,5 = 101 , 3 = 011,,,Jadi 653(8) = 110101011(2)

678(8) = ( langkah pertama harus dikonversikan terlebih dahulu ke desimal )

678(8) = 6×82  7×81  8×80 = 6×64 + 7×8 + 8×1 = 384 + 56 + 8 = 440(10)

440(10) = ( langkah kedua langsung mengubahnya kebiner )

440(10) = 440:2=220 sisa 0

220:2=110 sisa 0

110:2=55 sisa 0

55:2=27 sisa 1

27:2=13 sisa 1

13:2=6 sisa 1

6:2=3 sisa 0

3:2=1 sisa 1

1:2=0 sisa 1

dibaca dari bawah keatas ,jadi 440(10) = 110111000(2)

Jadi , 678(8) = 110111000(2)

*Oktal ke Hexadesimal

Caranya kita harus mengubahnya ke bilangan desimal dahulu baru dari desimal kiata ubah ke hexadesimal .

Contoh:

678(8) = 6×82  7×81  8×80 = 6×64 + 7×8 + 8×1 = 384 + 56 + 8 = 440(10)

440(10) = 440:16= 27 sisa 8

27:16= 1  sisa 11/B

1:16= 0 sisa 1

dibaca dari bawah keatas Jadi,  440(10) = 1B8(16)

Jadi ,hasil dari 678(8)  = 1B8(16)

Desimal

*Desimal ke Biner

Kita hanya tinggal membagi angka desimalnya dengan angka 2 dan hasilnya tidak ada koma ,tapi kita tulis saja berapa sisanya .

Contoh :

440(10) = 440:2=220 sisa 0

220:2=110 sisa 0

110:2=55 sisa 0

55:2=27 sisa 1

27:2=13 sisa 1

13:2=6 sisa 1

6:2=3 sisa 0

3:2=1 sisa 1

1:2=0 sisa 1

dibaca dari bawah keatas ,jadi 440(10) = 110111000(2)

*Desimal ke Oktal

Kita hanya tinggal membagi angka desimalnya dengan angka 8 dan hasilnya tidak ada koma ,tapi kita tulis saja berapa sisanya.

Contoh :

440(10) = 440:8= 55 sisa 0

55 :8=  6 sisa 7

7 :8=  0 sisa 7

dibaca dari bawah keatas ,jadi 440(10) = 770(8)

*Desimal ke Hexadesimal

Caranya yaitu hanya tinggal membagi angka desimalnya dengan angka 16 dan hasilnya tidak ada koma ,tapi kita tulis saja berapa sisanya.

440(10) = 440:16= 27 sisa 8

27:16= 1  sisa 11/B

1:16= 0 sisa 1

dibaca dari bawah keatas Jadi,  440(10) = 1B8(16)

Hexadesimal

*Hexadesimal ke Biner

Kita hanya tinggal menyekat 1 bilangan Hexadesimal lalu mengubahnya ke biner.

Contoh:

B4645(16) = B  4  6  4  5 = 1011  0100  0110  0100 0101(2)

*Hexadesimal ke Desimal

Kalikan setiap bit bilangannya dengan 16n , n adalah nilai pangkat tertinggi MSB berarti pangkatnya paling besar sedangkan LSB pangkatnya paling kecil atau = 0, hasilnya lalu jumlahkan .

Contoh :

1B8(16) = 1×162+Bx161+8×160 =256+176+8=440(10)

*Hexadesimal ke Oktal

Bilangan Hexa tidak bisa langsung dikonversikan ke oktal ,ubah dulu ke desimal lalu dari desimal bisa langsung dikonversikan ke oktal.

Contoh :

1B8(16) = 1×162+Bx161+8×160 =256+176+8=440(10)

440(10) = 440:8= 55 sisa 0

55 :8=  6 sisa 7

7 :8=  0 sisa 7

dibaca dari bawah keatas ,jadi 440(10) = 770(8)

Jadi , 1B8(16) = 770(8)

Sebagai penyearah tegangan, dioda digunakan untuk mengubah tegangan bolak-balik (AC) menjadi tegangan searah(DC). Penyearah tegangan ini ada 2 macam, yaitu :
1. Penyearah setengah gelombang (half-wave rectifier)
2. Penyearah gelombang penuh (full-wave rectifier)

1. Penyearah setengah gelombang (half-wave rectifier)
Saat digunakan sebagai penyearah setengah gelombang, dioda menyearahkan tegangan AC yang berbentuk gelombang sinus menjadi tegangan DC hanya selama siklus positif tegangan AC saja. Sedangkan pada saat siklus negatifnya, dioda mengalami panjaran balik (reverse bias) sehingga tegangan beban (output) menjadi nol.

Pada contoh diatas, anggaplah Vin sebagai tegangan input rangkaian setelah diturunkan oleh transformator yang mempunyai nilai sebesar 20Vpp atau 7,071V_RMS. Setelah disearahkan menggunakan dioda maka akan di dapat nilai tegangan DC atau nilai rata-ratanya.


Dari hasil simulasi dengan contoh perhitungan diatas terlihat bahwa terdapat perbedaan nilai. Hal ini bisa disebabkan karena komponen pada simulasi tidak ideal dan ini juga bisa terjadi pada percobaan secara langsung. Nilai tegangan yang ditunjukkan pada multimeter adalah nilai komponen AC (V_AC) atau DC (V_DC) saja. Sementara, untuk mengetahui tegangan puncak ke puncak (Vpp) diperlukan pengukuran menggunakan osiloskop atau bisa juga dengan perhitungan setelah VAC sudah diketahui.
Catatan : V_AC = V_RMS = V_EFEKTIF

2. Penyearah gelombang penuh (full-wave rectifier)
Saat digunakan sebagai penyearah gelombang penuh, dioda secara bergantian menyearahkan tegangan AC pada saat siklus positif dan negatif. Penyearah gelombang penuh ada 2 macam dan penggunaannya disesuaikan dengan transformator yang dipakai. Untuk transformator biasa digunakan jembatan dioda (dioda bridge) sementara untuk transformator CT digunakan 2 dioda saja sebagai penyearahnya.
a. Penyearah gelombang penuh dengan jembatan dioda (dioda bridge)
Pada dioda bridge, hanya ada 2 dioda saja yang menghantarkan arus untuk setiap siklus tegangan AC sedangkan 2 dioda lainnya bersifat sebagai isolator pada saat siklus yang sama. Untuk memahami cara kerja dioda bridge, perhatikanlah kedua gambar berikut.

Saat siklus positif tegangan AC, arus mengalir melalui dioda B menuju beban dan kembali melalui dioda C. Pada saat yang bersamaan pula, dioda A dan D mengalami reverse bias sehingga tidak ada arus yg mengalir atau kedua dioda tersebut bersifat sebagai isolator.

Sedangkan pada saat siklus negatif tegangan AC, arus mengalir melalui dioda D menuju beban dan kembali melalui dioda A. Karena dioda B dan C mengalami reverse bias maka arus tidak dapat mengalir pada kedua dioda ini.

Kedua hal ini terjadi berulang secara terus menerus hingga didapatkan tegangan beban yang berbentuk gelombang penuh yang sudah disearahkan (tegangan DC). Grafik sinyal dari penyearah gelombang penuh dengan jembatan dioda (dioda bridge) ditunjukkan seperti pada gambar berikut

Jembatan dioda (dioda bridge) tersedia dalam bentuk 1 komponen saja atau pun bisa dibuat dengan menggunakan 4 dioda yang sama karakteristiknya. Yang harus diperhatikan adalah besar arus yang dilewatkan oleh dioda harus lebih besar dari besar arus yang dilewatkan pada rangkaian.

b. Penyearah gelombang penuh menggunakan 2 dioda
Seperti telah disebutkan diatas, penyearah gelombang penuh menggunakan 2 dioda ini hanya bisa digunakan pada transformator CT, dimana tegangan sekunder yang dihasilkan oleh trafo CT ini adalah :

dimana V1=teg primer dan V2=teg sekunder
Cara kerja penyearah gelombang penuh jenis ini dapat dijelaskan seperti berikut :

Pada artikel mengenai trafo diketahui bahwa pada bagian sekunder trafo CT terdapat 2 sinyal output yang terjadi secara bersamaan, mempunyai amplitudo yang sama namun berlawanan fasa. Saat tegangan input (teg primer) berada pada siklus positif, pada titik AO akan terjadi siklus positif sementara pada titik OB akan terjadi siklus negatif. Akibatnya D1 akan mengalami panjaran maju (forward bias) sedangkan D2 mengalami panjaran balik (reverse bias) sehingga arus akan mengalir melalui D1 menuju ke beban dan kembali ke titik center tap.

Saat tegangan input (teg primer) berada pada siklus negatif, pada titik AO akan terjadi siklus negatif sementara pada titik OB akan terjadi siklus positif. Akibatnya D2 akan mengalami panjaran maju (forward bias) sedangkan D1 mengalami panjaran balik (reverse bias) sehingga arus akan mengalir melalui D2 menuju ke beban dan kembali ke titik center tap.

Dari penjelasan cara kerja penyearah gelombang penuh jenis ini terlihat bahwa tegangan yang terjadi pada beban mempunyai polaritas yang sama tanpa memperdulikan dioda mana yang menghantar karena arus mengalir melalui arah yang sama sehingga akan terbentuk gelombang penuh yang disearahkan seperti ditunjukkan pada grafik sinyal berikut.